当人类跨进了人工智能的时代,实际上也就是进入了与数字打交道的时代。尽管大部分的人,都不知道电脑0/1的数字系统是怎么运作的,但现在显现在人们面前的每一样东西,几乎都是直接或间接地跟电脑的数字系统连在一起的。
也就是说,当人类进入了数字时代的时候,上天必定会在数字的领域为人类揭开越来越多的奥秘,以便让科学家们能够快马加鞭地把人类文明推向一个崭新的阶段。
为此,在这样关键的时刻,我们就不得不提一下所谓数根的问题,以供有识之士做进一步的思考和探索。
所谓的“数根”是近些年来才出现的一个词语,它和“树根”刚好是同音字。每一个数字的后面都有一个“根”,就像每一棵树都有根一样,所以给它起了一个名叫“数根”。
然而,数根和树根不同的地方在于,每一棵树的根各不相同,千千万万棵不同的树,就有千千万万种形状各异的树根。但是数根却不一样,纵然千千万万的数字各不相同,但归纳起来总共却只有9个数根。

数根是采用一种叫“三一归根法”的方式计算出来的。不管天下的数字有多少,照着这种方法所计算出来的数根,归纳起来总共就只有如下九个:
1,
371,
153,
370,
407,
(133_55_250),
(217_352_160),
(1459_919),
(244_136)
这九个数根,可以分为两大类:第一类是每个数根只由一个固定不变的数字构成,被称为不变数根,如上列数根中不加括号的五个数字,都是不变数根。
第二类是每个数根包含了两个或三个数字,被称为循环数根,如上列数根中加括号的四个,都是循环数根。显而易见,循环数根的特点就是数根中的两个或三个数字,就像落在一个圈子里,走马灯式地不停变着走,永无止息。
下面,为你展示一下数根的运算过程:

由此,我们得到第一个不变的单元数根——1。

由此,我们得到第二个单元数根——371。

由此,我们得到第三个单元数根——153。

由此,我们得到第四个单元数根——370。

由此,我们得到第五个单元数根——407。

由此,我们得到第六个数根,也是第一个三元数根——(133_55_250)。

由此,我们得到第七个数根,也是第二个三元数根——(217_352_160)。

由此,我们得到第八个数根,也是第一个二元数根——(1459_919)。
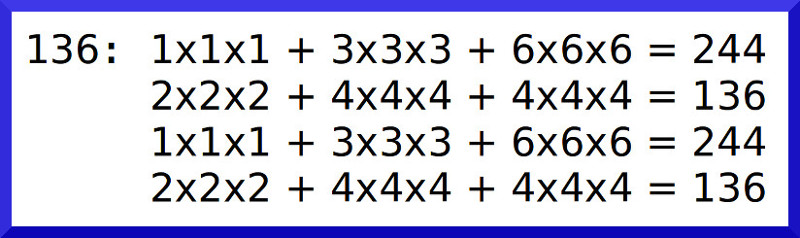
由此,我们得到最后一个数根,就是第九个数根,同时它也是第二个二元数根——(244_136)。
如果你由136后面的数字作归根的起始点再继续演算下去,得到的不过是上面九个数根的其中任何一个,而不会再出现新的数根了。






0 条评论